Andrew Shaw

Blog » Resorting Pages with Graphs

2025-01-15 advent-of-code graph-theory internet

There's a really neat graph-based solution to Day 5 of 2024's Advent of Code.

I'm going to really heavily paraphrase, so you should read the problem spec if this is unclear. Essentially, we're given a list of 'page updates', as pairs of page IDs, for example:

47|53
97|13
97|61

Which means "page 47 must occur before 53, page 97 before 13, page 97 before 61".

The next set of inputs are proposed sets of page orderings:

97,61,53,29,13
75,29,13,97

So in line one, we place page ID 75, then page ID 47, ... etc.

Part one of the problem is to find the orderings which are valid. So, given the set of rules we just ingested, check that the proposed orderings don't break any of those rules. For example, the second one is invalid, since the last placement tells us to put page 97 after page 13, but our rules say 97 must always occur before 13.

In the second part, we're asked to take all of the ones which are invalid, and then put them in the right order according to our rules.

Naively, I started doing something like the following, take the rules as literal Prolog facts:

before(74, 53).
before(97, 13).
before(97, 61).

Then checking the validity involves some sort of search. This encoding is incomplete though, since if we query before(X, Y) we only get solutions for if X and Y are directly adjacent.

three node graph with edges, showing a thinner edge from the first to the last node

We're missing the fact that $a$ coming before $b$ is valid; the thin edge in the graphic above.

We can add another predicate:

before(X, Y) :-
    before(X, A),
    before(A, Y).

This captures the idea that X appears before Y if we have some A which X is before, and that A itself is before Y (either as a direct match to one of the earlier facts, or as a recursive call to this rule.

Then we can validate an ordering by taking pairwise entries, and checking it's correct by querying before/2.

This should work, but is still a bit too unidirectional. I'm not quite a good enough Prolog programmer to take this further (in the given day's time to solve the challenge), so I switched gears to Elixir. As is usually the case, if we can find a better representation of our data, the mechanics of the solution should hopefully just fall out.

We can rephrase the problem to be a bit more formal. Let's define:

The set of page ids $I$, which in our case is just integers, but these can be arbitrary labels.
The set of rules $R$, which are pairs of page IDs $(a, b)$, indicating that $a$ must appear before $b$.
The set of orderings $O$, which is a proposed ordering of page IDs.

Now here's the graph bit, we can read $R$ to be a set of edges on a directed graph $G$, where $(a, b)$ indicates $a$ appearing before $b$. The graph $G$ now encodes quite some detail:

What page IDs are covered
What page IDs are directly adjacent
What page IDs may appear before another

The last part is the cool part - $(a, b)$ is valid if $b$ is reachable from $a$, that is you can walk a path from a going through arbitrarily many nodes along the way, and end up at $b$ (what our rule before/2) encoded earlier.

Using LibGraph for Elixir (and having turned the input into a graph as the "parse" step made the solution to part A stupidly succinct:

Enum.filter(updates, &Graph.is_subgraph?(&1, ordering))

The ordering being a subgraph of the updates is expressing that all of the nodes in ordering have to appear in the same order as defined by updates, as explained above.

Another way to conceptualise graph H being a subgraph of graph G, is if we can remove intermediate nodes from G to eventually arrive at H:

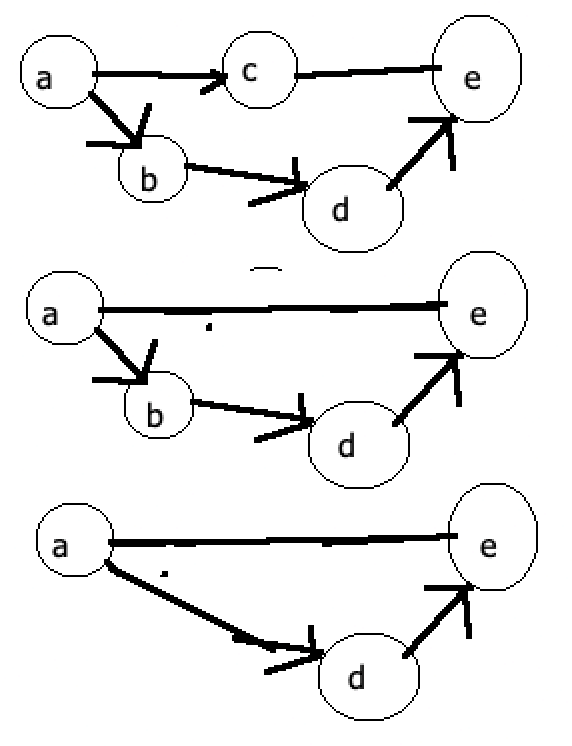
sucessively removing vertices of G to make H

The second part asks us to fix the out-of-order orderings, per the rules. This again ends up being really simple when modelled as graphs:

updates
|> Enum.reject(&Graph.is_subgraph?(&1, ordering))
|> Enum.map(fn g ->
    g
    |> Graph.vertices()
    |> then(&Graph.subgraph(ordering, &1))
    |> Graph.topsort() 
end)

We first filter out the ones that are correct, then perform a topological sort on the vertices of the updates which appear in the ordering. A topological sort is what it sounds like, rather than sorting e.g. by some comparator, we sort them by the order in which they show up in the graph. Essentially, walk it from the start to the end, listing out the edges as you see them.

And that's about it! I've probably not explained this too well, but I thought it was really neat. The full code for the solution is on my GitHub repo which contains partial solutions for the rest of 2024. Onward to more graphs.